Getting a Little Further Than Hello World With Rust - Part 3: Concurrency & Parallelism
This is the third post of Getting a Little Further Than Hello World With Rust series. We will look into Rust’s concurrency support. I intend to provide a guide for the Rust language and try to keep things within the safe Rust realm. We will be looking at the concurrency primitives that are in the Rust standard library. Please keep in mind that there are popular libraries that provide other efficient and convenient concurrency primitives.
Rust’s concurrency model relies heavily on the type system and borrow checker to prevent concurrency related issues at compile time. There are two traits that classify what can be done with a type in a multi-threaded program. These are Send & Sync. We will not go into the specifics in this post, but do not worry, compiler provides good feedback regarding these traits as you use them.
QuickSort
We will be implementing a single-threaded and a parallel version of quicksort sorting algorithm in this post. Quicksort algorithm can be summarized as below:
- Pick a pivot element.
- Arrange the collection elements in three consequtive groups:
- Elements lower than the pivot element (unsorted)
- Repetitions of pivot
- Elements higher than the pivot.
- Apply quicksort to the first and third groups above.
I am sure you have noticed once we are done sorting the lower and higher group, which would apply the algorithm recursively, the entire collection will be sorted. Quicksort is a divide and conquer algorithm. This quality allows us to use parallelism. Third step, sorting of higher and lower groups can be run in parallel without affecting the result of each other.
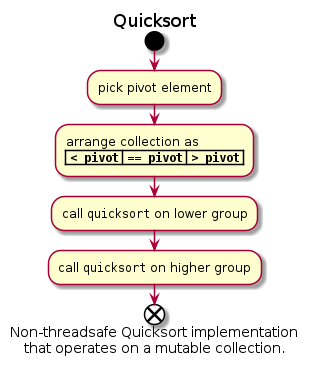
Non-Threadsafe Implementation
Our reference implementation of quicksort will operate on a mutable slice:
pub fn quicksort_mut<T: Ord + Clone>(coll: &mut [T]) {
unimplemented!(); // we will fill in the body later
}
Note that there is no return type in the signature of the method above. Also we require type T to implement Ord to enable comparison and Clone to be able to create copies of elements. We will need these type bounds later.
quicksort_mut does not need do anything if coll is empty or it has only one element:
pub fn quicksort_mut<T: Ord + Clone>(coll: &mut [T]) {
if coll.len() > 1 {
unimplemented!();
}
}
For slices with at least two elements quicksort_mut first arranges the element with respect to the pivot and then recursively calls itself on the lower and higher groups:
pub fn quicksort_mut<T: Ord + Clone>(coll: &mut [T]) {
if coll.len() > 1 {
let (left_idx, right_idx) = organize(coll);
quicksort_mut(&mut coll[0..left_idx]);
quicksort_mut(&mut coll[right_idx..]);
}
}
We can see a powerful feature of Rust in action on highlighted line above; destructuring. organize returns a (usize, usize), that is a two-tuple of a usize and another usize. We are assigning them to individual variables constants.
We will look into organize soon. But before we do that, please note two recursive calls to quicksort_mut that create (sub)slices on coll one after the other. This works because these call are borrowing coll, there is no move here. Before we get to make the second recursive call, first borrow is returned. Let us look at organize now:
fn organize<T: Ord + Clone>(coll: &mut [T]) -> (usize, usize) {
// Preparation
// Copying to temp vector
// Copying back to original slice
// Result
unimplemented!();
}
Quicksort implementations commonly modify the collection by swapping two elements at a time. I admit swap-based implementations are more space efficient and significantly faster for element types (T) with expensive clone implementations. However I have chosen, for better readability, to create a temporary vector with the elements organized and then copy the elements back to the input slice, cloning each element two times in the process. Once you have a good grasp of the language you can implement much a better quicksort and scoff at my code.
// This is the preparation section of organize:
let n = coll.len();
let mid: T = coll[(n / 2)].clone();
let mut result: Vec<T> = vec![mid.clone(); n];
let mut left_idx = 0;
let mut right_idx = n - 1;
mid is our pivot value. When we create result vector, we seed it with the value of mid. left_idx and right_idx refer to the positions in result (and later in coll) where lower group ends and where higher group starts.
// This is where we build the temporary vector:
coll.iter().for_each(|i| {
if i < &mid {
result[left_idx] = i.clone();
left_idx += 1;
} else if i > &mid {
result[right_idx] = i.clone();
right_idx -= 1;
}
});
Above code snippet showcases another strength of Rust; closures. Iterator.for_each takes an anonymous function to run on each element of the coll.
Since we have seeded result with the value of mid, if i == mid we can just choose to do nothing for that element i. For each i where i < mid we insert the value of i into result at left_idx and then increment left_idx. If i > mid, we use right_idx position to insert and then decrement right_idx. Remember right_idx started pointing to the last element and moves left (decremented) after each insert.
// Copying temporary vector into coll and return indices
result.iter().enumerate().for_each(|(i, elem)| {
coll[i] = elem.clone();
});
return (left_idx, right_idx);
Above is the last piece of code we need to complete organize. This function needs to communicate three things to outside world; organized collection and the two pointers we return. This may be confusing for people coming from functional languages which emphasize immutable values as it mutates coll. It may also be confusing for programmers who are accustomed to the imperative style as left_idx and right_idx are not also mutable pointers passed to organize. My rationale of returning left_idx and right_idx is two-fold; they are generated within organize and more importantly this way they are immutable. Keeping this that do not need to mutate immutable is a good practise as it prevents accidental modification. Below is the full listing of both quicksort_mut and organize:
pub fn quicksort_mut<T: Ord + Clone>(coll: &mut [T]) {
if coll.len() > 1 {
let (left_idx, right_idx) = organize(coll);
quicksort_mut(&mut coll[0..left_idx]);
quicksort_mut(&mut coll[right_idx..]);
}
}
fn organize<T: Ord + Clone>(coll: &mut [T]) -> (usize, usize) {
let n = coll.len();
let mid: T = coll[(n / 2)].clone();
let mut result: Vec<T> = vec![mid.clone(); n];
let mut left_idx = 0;
let mut right_idx = n - 1;
coll.iter().for_each(|i| {
if i < &mid {
result[left_idx] = i.clone();
left_idx += 1;
} else if i > &mid {
result[right_idx] = i.clone();
right_idx -= 1;
}
});
result.iter().enumerate().for_each(|(i, elem)| {
coll[i] = elem.clone();
});
return (left_idx, right_idx);
}
Note that using return is optional in Rust if the return value is in tail position. Last line can also be written as (left_idx, right_idx) (without the semicolon).
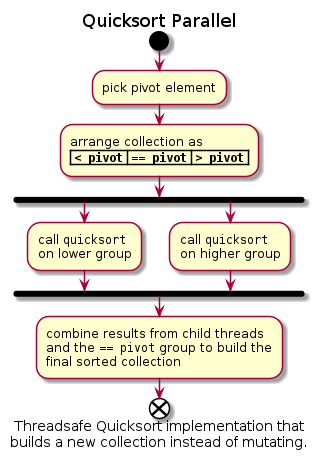
Parallel Implementation
Now that we have a reference implementation of the algorithm that runs on a single thread, we can start thinking about the parallelization. Here are the tools we will be using to create the parallel version:
use quicksort::mutable::quicksort_mut;
use std::cmp::Ord;
use std::sync::mpsc::{self, Receiver};
use std::thread;
We will use std::thread to divide the work into smaller chunks. When the unit of work is too small to justify spawning a thread we will fall back to quicksort_mut. We will be using channels (mpsc) to communicate between the threads. Finally we need to constrain our element type to be Ord to be able to do comparison.
Our entry point for the parallel quicksort will have the following signature:
pub fn quicksort<T: Ord + Clone + Send + 'static>(coll: &[T]) -> Vec<T>
Note that we are returning a value (Vec<T>) this time. Also note that input is of slice of T type. Instead of forcing callers to provide vectors we are using a fundamental Rust abstraction; slice. This enables caller to pass vectors or anything else that can be turned into a slice.
quicksort implementation is quite simple, it just calls quicksort_inner with the coll and 0 as depth:
pub fn quicksort<T: Ord + Clone + Send + 'static>(coll: &[T]) -> Vec<T> {
quicksort_inner(coll, 0)
}
Depth is used to limit the number of threads spawned. Every partition of the coll either sorts itself using the mutable implementation or spawns two threads after calling organize in the current thread. There are two constants that help determine which of these will happen:
const MUT_THRESHOLD: usize = 2 ^ 16;
const MAX_DEPTH: usize = 5;
MUT_THRESHOLD determines the minimum size of a partition that can spawn new threads. Partitions below this size (65536 elements) are sorted using quicksort_mut.
MAX_DEPTH is the other constant we will use to limit the number of threads spawn. If we set MAX_DEPTH as 3 we would have 15 (8 + 4 + 2 + 1) threads running simultaneously as worst case. Worst case count for 5 is 63. Since my machine does not have so many cores and also organize takes some time to run I expect some of the branches to complete their work before all threads are spawned. So in the typical scenario there should be less number of simultaneously running threads.
Above strategy is implemented in quicksort_inner as below:
fn quicksort_inner<T: Ord + Clone + Send + 'static>(coll: &[T], depth: usize) -> Vec<T> {
let n: usize = coll.len();
if n > 1 {
if n < MUT_THRESHOLD || depth >= MAX_DEPTH {
// sort using mutable algorithm
} else {
// sort using parallel algorithm
}
} else {
coll.to_vec()
}
}
If the collection is empty or contains only one element we return a copy of it. If the collection has two or more elements we choose the mutable or parallel algorithm based on the two conditions I have mentioned above. The mutable algoritm is just a straightforward wrapper around quicksort_mut. Since the input collection is a read-only slice, we create a copy of it, drop the input slice, sort the copied vector in place and then return it:
let mut result: Vec<T> = coll.to_vec();
drop(coll);
quicksort_mut(&mut result);
result
Interesting part is the parallel algorithm:
let (left, right, center, center_count) = split(coll);
drop(coll);
let left_rx = execute_in_thread(left, depth + 1);
let right_rx = execute_in_thread(right, depth + 1);
thread::yield_now();
let left_result: Vec<T> = left_rx.recv().unwrap();
let right_result: Vec<T> = right_rx.recv().unwrap();
join(n, left_result, right_result, center, center_count)
First two lines perform the organize step and drop the input slice immediately. split is a bit more specialized version of organize, we will look at it next. Next three lines spawn the new threads and assign the receivers to listen to left_rx and right_rx. Last three lines block on the receivers and build the final result. We will look at execute_in_thread and join after we go through the code of split.
Main difference between organize and split is that latter mutates the input whereas former builds new vectors by cloning items:
#[inline]
fn split<T: Ord + Clone>(coll: &[T]) -> (Vec<T>, Vec<T>, T, usize) {
assert!(!coll.is_empty());
let n: usize = coll.len();
let mid: T = coll[(n / 2)].clone();
let cap: usize = n * 2 / 3;
let mut left: Vec<T> = Vec::with_capacity(cap);
let mut right: Vec<T> = Vec::with_capacity(cap);
coll.iter().for_each(|i| {
if i < &mid {
left.push(i.clone());
} else if i > &mid {
right.push(i.clone());
}
});
let mid_count: usize = n - left.len() - right.len();
return (left, right, mid, mid_count);
}
Since middle element will be the same value no matter how many times it repeats we do not neet to build a vector for it and just return an extra value for the number of repetitions. Notice that split’s return type is a tuple. I did not bother creating a struct for this function that is intended to be called only internally.
Let us take a look the function that lies at the heart of this implementation:
fn execute_in_thread<T: Ord + Clone + Send + 'static>(
coll: Vec<T>,
depth: usize,
) -> Receiver<Vec<T>> {
let (sender, receiver) = mpsc::channel();
thread::spawn(move || {
sender.send(quicksort_inner(&coll, depth)).unwrap();
});
return receiver;
}
As I have mentioned above we will be using thread::spawn to create threads and mpsc::channel abstraction to communicate between threads. spawn is straightforward:
thread::spawn(move || { ... });
Using a move closure prevents borrowing from the surrounding scope. Borrow checker would not be able to ensure safety in this case due to non-deterministic nature of multi-threaded execution. Rust compiler inserts code to free the memory for owned values at the end of their lifecycle. This means if the owned value is not returned from the enclosing function, it will be freed. But the thread is unlikely to complete its work before the enclosing function returns. It probably will not even start executing. Moving the value inside the closure prevents the remainder of the enclosing function from using the value, but it deterministically enables the compiler to manage the lifecyle of the value.
mpsc::channel returns two handlers on a channel, one for sending messages (sink) and one for receiving (source). We moved the sink into the new thread created. Once the call to quicksort_inner completes, the results are sent through the channel, to whomever is listening. The receiver, a.k.a. source, is returned from execute_in_thread. So the listener is the original thread that spawns the new thread in this case. Let us refer to the parallel execution strategy again, it launches two new threads, wait for their completion, pick up the result and stitch them together:
let left_rx = execute_in_thread(left, depth + 1);
let right_rx = execute_in_thread(right, depth + 1);
thread::yield_now();
let left_result: Vec<T> = left_rx.recv().unwrap();
let right_result: Vec<T> = right_rx.recv().unwrap();
join(n, left_result, right_result, center, center_count)
Note that we can wait for a thread to complete its work by calling join on the JoinHandle returned by thread::spawn. In our case we do not care so long as the channel produces one message. mpsc stands for multi producer single consumer, and the channel abraction this module provides support sending multiple messages. We only needed to send one message after the whole work (for the thread) is done.
Final piece of the puzzle is the join function. Joining algorithm is same as mutable version, we create a new vector and copy elements into the right indices. There is only the minor difference of copying from two separate vectors (left & right below) as opposed to a single vector.
#[inline]
fn join<T: Ord + Clone>(
n: usize,
left: Vec<T>,
right: Vec<T>,
center: T,
center_count: usize,
) -> Vec<T> {
let mut result: Vec<T> = vec![center; n];
for (idx, i) in left.iter().enumerate() {
result[idx] = i.clone();
}
let offset = left.len() + center_count;
for (idx, i) in right.iter().enumerate() {
result[idx + offset] = i.clone();
}
result
}
Performance Comparison
After working on the parallel algorithm I have created some benchmarks. Results have shown that the parallel version performed much worse for collections of 10.000 elements, slightly worse for collections of 100.000 elements and it had more or less same performance for collections of 1 million elements. There two reasons for this lack of performance improvement. Firstly the algorithm we have chosen is not particularly computationally heavy. Most operations are about assigning work rather than doing the work. And doing the work is essentially comparing two elements. Second reason is our parallel code is not well optimized.
Allocation and copying are costly operations. Both parallel and mutable versions do allocation and copying that can be optimized away. Parallel version requires more allocating and copying. There is nothing much we can do about the copy happening within split since we have decided to not pursue a swap oriented implementation. However we can use a more efficient copy operation that Vec supports in join:
#[inline]
fn join<T: Ord + Clone>(
n: usize,
left: &mut Vec<T>,
right: &mut Vec<T>,
center: T,
center_count: usize,
) -> Vec<T> {
let mut result = Vec::with_capacity(n);
result.append(left);
result.append(&mut vec![center; center_count]);
result.append(right);
result
}
Another expensive operation is spawning threads. We can reduce the number of threads spawned by doing half of the work in the parent thread:
fn quicksort_inner<T: Ord + Clone + Send + 'static>(coll: &[T], depth: usize) -> Vec<T> {
let n: usize = coll.len();
if n > 1 {
if n < MUT_THRESHOLD || depth >= MAX_DEPTH {
let mut result: Vec<T> = coll.to_vec();
drop(coll);
quicksort_mut(&mut result);
result
} else {
let (left, right, center, center_count) = split(coll);
drop(coll);
let right_rx = execute_in_thread(right, depth + 1);
thread::yield_now();
let mut left_result: Vec<T> = quicksort_inner(&left, depth+1);
let mut right_result: Vec<T> = right_rx.recv().unwrap();
join(n, &mut left_result, &mut right_result, center, center_count)
}
} else {
coll.to_vec()
}
}
There are surely other ways we can optimize the code and get better performance. For example we can consume the input vector without freeing the underlying memory and use it to build vectors to be moved into child treads. Or we can use a threadpool to avoid paying the cost of thread creation. I will stop here because this is an introductory post. Two optimizations mentioned above improved the performance about 15%.
If you have any questions, suggestions or corrections feel free to drop me a line.